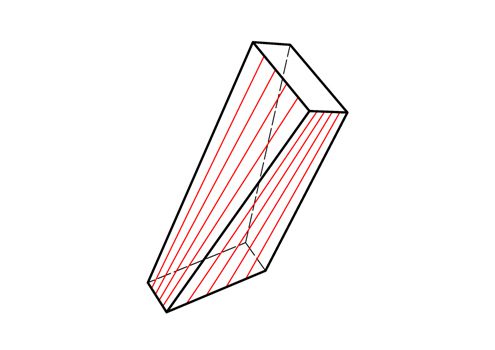
Superfici rigate
Cosa sono le superfici rigate?
Le superfici rigate sono delle superfici ottenute dall’unione di più linee rette: si possono generare superfici rigate facendo scorrere i due estremi di un segmento di retta lungo due curve. Avete mai provato a stringere in mano degli spaghetti? In alcuni casi questi si dispongono nello spazio occupando un volume maggiore agli estremi, e disegnando due cerchi con le punte. In questo caso gli spaghetti sono proprio delle “righe”, le quali, sistemandosi lungo i due cerchi agli estremi, formano una superficie dotata di curvatura, pur essendo singolarmente rettilinei.

Gli spaghetti si distribuiscono formando una superficie rigata chiamata “iperboloide”.
Tanto più fitte sono le linee della rigata, tanto più la superficie sarà ben definita; analizziamo, ad esempio, il cono nella figura che segue: un numero limitato di righe lo rende più simile ad un cono a base poligonale, quindi privo di curvatura. Incrementando la quantità di segmenti, la superficie si definisce sempre più; un numero infinito determina una superficie continua e “perfetta”.
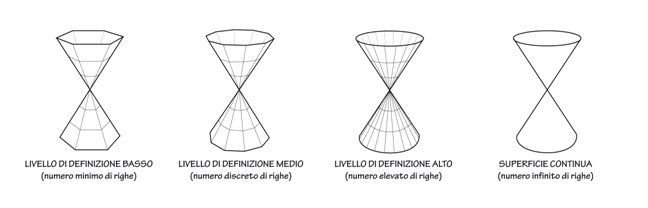
Un cono generato da righe: un numero di segmenti maggiore aumenta il livello di “definizione” della superficie continua.
Da una forma all’altra.
Il motivo per il quale le superfici rigate trovano facile applicazione in Architettura, ed in particolare nelle opere nerviane, è la possibilità di ottenere curvature complesse partendo da semplici linee rette.
Un esempio di superficie all’apparenza complessa ma in realtà molto semplice poiché composta da sole righe intrecciate, è quella definita “paraboloide”.

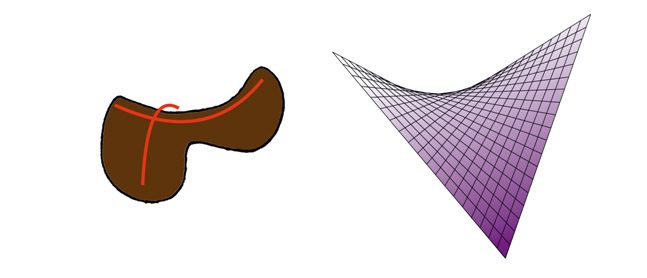
Le selle dei cavalli hanno la forma di un paraboloide, una superficie curva ottenibile mediante un numero elevato di segmenti con diversa inclinazione.
Un altro aspetto importante relativo al metodo di “rigatura”, riguarda la possibilità di generare solidi e superfici che congiungono curve o forme geometriche differenti.


Nello spazio tridimensionale, collegare due figure piane come un cerchio ed un quadrato può sembrare difficoltoso; mediante una fitta rigatura, però, è possibile ottenere un solido avente sezione di forma differente in ogni suo punto.
Due superfici rigate notevoli, qui indicate a titolo esemplificativo, sono il “tronco di cono”, generato congiungendo due cerchi di diametro differente, ed il “conoide”, ottenuto collegando un arco ed una linea retta.
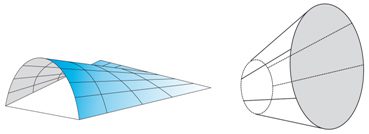
Conoide (a sinistra) e tronco di cono (a destra) ottenibili tramite la “rigatura”.
In Natura, dove ritroviamo le superfici rigate?
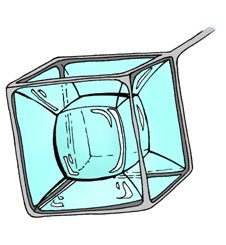
In Natura è possibile trovare le rigate sia in elementi prettamente naturali, sia in quelli derivanti da azioni artificiali. In particolare, è molto interessante il legame tra le superfici rigate e quelle cosiddette “minime”. Le superfici minime hanno la peculiarità di essere quelle con la minor estensione possibile a parità di curve ai bordi; per capire meglio questo concetto, analizziamo un classico esperimento che viene generalmente eseguito con l’acqua saponata: se immergiamo un anello in una bacinella piena di acqua e sapone, si formerà all’interno dell’anello una lamina liquida. La superficie formata dalla lamina è un piano, e costituisce una superficie minima in quanto qualsiasi altra geometria, per esser generata, avrebbe avuto bisogno di una maggior quantità di liquido. Lo stesso esperimento può eseguirsi immergendo nell’acqua saponata un telaio di diverse forme, ed ottenendo superfici minime in quanto la lamina elastica di sapone si tende sul telaio ricoprendo la minore estensione possibile. Tuttavia, solo alcune superfici minime ottenibili con il sapone risultano essere anche rigate; una superficie che sia contemporaneamente minima e rigata rappresenta senza dubbio una geometria super-economica, poiché più facile da costruirsi geometricamente, ed al contempo bisognosa di minor materiale per esser realizzata. Questo dimostra ancora una volta la capacità della Natura di sapersi adattare alle esigenze con il minor sforzo possibile.
Per maggiori dettagli sulla capacità della natura di minimizzare le superfici, leggi la scheda LA RIPETIZIONE SERIALE!
Le superfici rigate nelle opere di Pier Luigi Nervi
Nelle sue opere, Nervi ricorre spesso a forme aventi “curvatura singola”, ossia superfici che risultano curve se sezionate lungo una direzione principale, ma rettilinee se sezionate lungo l’altra direzione. Ne consegue che queste superfici sono rigate, in quanto il segmento costituente la sezione rettilinea scorre lungo la sezione curva, generando la superficie. Due esempi particolari sono le falde delle Aviorimesse di Orbetello, e l’Aula per le udienze in Vaticano.
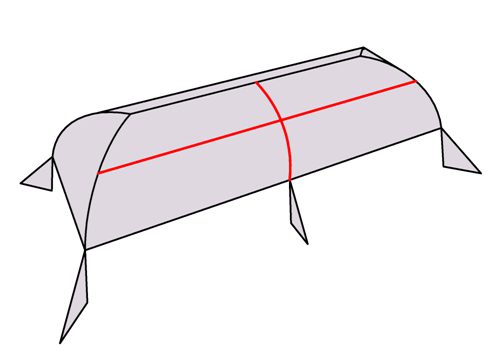
Schema geometrico delle aviorimesse di Orbetello: le falde possono essere ottenute mediante lo scorrimento di un segmento lungo una curva.
Nervi, tuttavia, utilizza le rigate non solo per grandi superfici, ma anche per i singoli elementi strutturali, in maniera tale da incrementarne le prestazioni meccaniche. I pilastroni che sorreggono la copertura dell’Aula per le udienze, ad esempio, sfruttano la rigatura per congiungere due rettangoli ruotati di 90°: in questo modo il pilastro risulta più adatto a resistere agli sforzi cui è sottoposto.